Quantum Pumping
(or how to generate a current at zero bias)
A direct current (dc) is usually associated to a dissipative flow of the electrons in response to an applied bias voltage. However, in systems of mesoscopic scale a dc current can be generated even at zero bias. This captivating quantum coherent effect is called quantum pumping (quantum charge pumping to be more precise). A device capable of providing such effect is called a quantum pump [1] .
For a closed system, the generation of a circulating current is called "Quantum stirring" [2] .
[Update: If you are interested in new ways of achieving one-way transport without time-dependent potentials check this.]
What's the hype about Quantum Pumping or Quantum Pumps?
(or why I believe that it's worth of attention)
Although of a different nature, Quantum Pumping has some similarities with other fascinating phenomena such as Persistent Currents and Superconductivity.
Quantum Pumping allows exploring fundamental issues regarding the role of different symmetries in transport.
A Quantum Pump may provide novel ways of reducing the dissipation of energy as wasteful heat, define a better current standard closing the metrological triangle, or even be used for quantum computing.
More recently, the development of carbon-based AC devices (carbon nanotubes and graphene) including quantum pumps is being pursued by many groups. You can get a flavor by checking the following articles and references therein:
- Quantum charge pumping in graphene-based devices: When lattice defects do help [pdf]
- Enhancing single-parameter quantum charge pumping in carbon-based devices [pdf]
- ac transport in graphene-based Fabry-Perot devices [pdf]
Is it possible to achieve Quantum Pumping with a single time-dependent parameter?
Within the adiabatic theory [1] , at least two out of phase time-dependent parameters (such as gate voltages) are needed to obtain a non-vanishing pumped current. What is the physics behind this condition? How would a "minimal" quantum pump look like? Is it possible to achieve a single-parameter quantum pump?
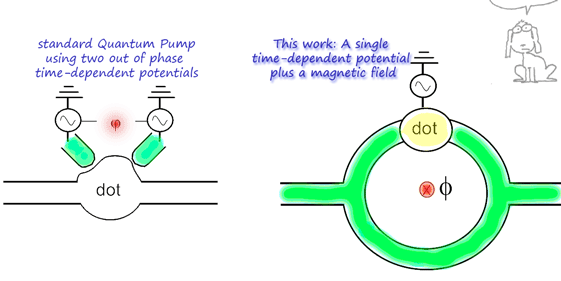
Scheme for a single parameter quantum pump (right) as considered in Phys. Rev. B 72, 245339 (2005) [5]. [The pet on the upper right corner is Mendieta, a character from the argentinean comic creator Roberto Fontarrosa.]
Interestingly, it is found that the direction of the pumped current can be reversed by reversing the direction of the magnetic field. This may be useful to separate pumping from other competing effect: rectification, which gives a dc current that is symmetric in the magnetic field.
Recently, such mono-parametric (or single parameter) quantum pumps were experimentally achieved [4].
Beyond model systems and down to graphene and nanotube devices.
(AC transport in carbon-based devices: challenges and perspectives)
An overview of current research on AC transport in carbon-based devices you can check Chapter 6 of Introduction to Graphene-Based Nanomaterials: From Electronic Structure to Quantum Transport (Cambridge University Press, January 2014). You may also check references 5-11 below. Promising lines include the influence of defects in the pumping of charge in graphene-based devices (a first study was presented in [10]) and the generation of topologically protected states in graphene [11].
References:
[1] P. W. Brouwer, Phys. Rev. B 58, R10135 (1998).
[2] See for example I. Sela and D. Cohen, Phys. Rev. B 77, 245440 (2008).
[3] L. E. F. Foa Torres, Phys. Rev. B 72, 245339 (2005). [pdf]
[4] B. Kaestner et al., Phys. Rev. B 77, 153301 (2008).
[5] L. E. F. Foa Torres and G. Cuniberti, C. R. Physique 10, 297 (2009).
[6] L. E. F. Foa Torres and G. Cuniberti, Appl. Phys. Lett. 94, 222103 (2009). [pdf]
[7] C. G. Rocha, L. E. F. Foa Torres and G. Cuniberti, Phys. Rev. B 81, 115435 (2010). [pdf]
[8] H. L. Calvo, H. M. Pastawski, S. Roche, and L. E. F. Foa Torres, Appl. Phys. Lett. 98, 232103 (2011). [pdf]
[9] L. E. F. Foa Torres, H. L. Calvo, C. G. Rocha, and G. Cuniberti Appl. Phys. Lett. (2011). [pdf]
[10] L. H. Ingaramo and L. E. F. Foa Torres, Applied Physics Letters, 103, 123508 (2013). [pdf]
[11] P. M. Perez-Piskunow, G. Usaj, C. A. Balseiro, and L. E. F. Foa Torres, http://arxiv.org/abs/1308.4362